SCS laboratoryの紹介
複雑系シミュレーション(CS)研究室では、複雑系の離散ミクロモデルの構築およびそれを用いたシミュレーションの研究を進めています。金融市場のゆらぎ、コロイドの自己会合、腫瘍の発生と成長を複雑系の典型例とし、4つの研究方向を設けています。
- マルチエージェント協調進化ゲームによる金融市場の解析
- 離散運動論モデルを用いた複雑流体のシミュレーション
- セルベースがんのモデル化とシミュレーション
- エージェントベースモデルを用いた技術・社会転移のシミュレーション
SCSとは
SCSの定義
SCSとはSimulation of Complex Systemsの略称で、即ち複雑系のシミュレーションである。
SCSという研究は、複雑性(Complexity)の物理、離散モデル(Discrete Models)の構築及び高性能計算(High Performance Computing)の技術に関連する学問分野である。
SCSの研究対象
SCSの研究対象は複雑系である。Wikipediaで調べば、
複雑系(ふくざつけい complex system)とは、多数の因子または未知の因子が関係してシステム全体(系全体)の振る舞いが決まるシステムにおいて、それぞれの因子が相互に影響を与えるために(つまり相互作用があるために)、還元主義の手法(多変量解析、回帰曲線等)ではシステムの未来の振る舞いを予測することが困難な系を言う。
https://ja.wikipedia.org/wiki/%E8%A4%87%E9%9B%91%E7%B3%BB
という冗長な定義がある。我々は、複雑系を構成する要素の特徴と系の複雑性の由来によって、
- 複雑物理系
- 複雑適応系
として複雑系を分類し、SCSの研究対象を説明している。
複雑物理系(Complex Physical Systems, CPS)
- 「粒子」で構成される複雑システム
- 膨大な数の単純要素から創発される複雑性
- 実例:多相流、非ニュートン流れ、コロイド、内部構造性流れ、ぬれ現象、横毛管力現象など
複雑適応系(Complex Adaptive Systems, CAS)
- 「エージェント」で構成される複雑システム
- 順応性を持つ要素から創発される複雑適応性
- 実例:金融市場、資源分配システム、電力市場、二酸化炭素排出権市場など
複雑物理系と複雑適応系の階層性構造
統計物理の視点から複雑物理系と複雑適応系に着目すると、共通する階層性構造を認識できる。
CPSの階層性構造
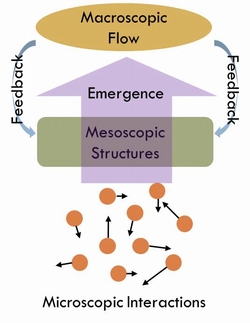
CASの階層性構造
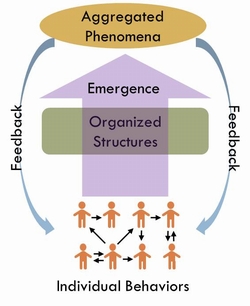
SCSのモデリング
コンピュータシミュレーションにとって、最も重要な一歩はシミュレーションの対象に対するモデル化(Modeling)である。我々は、モデルにおける時間、物理空間及び相空間(例えば、速度空間)の記述により、
- 連続モデル
- 離散モデル
としてシミュレーションモデルを分類している。従来の理工学領域で利用される主流的なモデリング手法は、微分方程式(PDE)や、確率過程(Stochastic Process)などの連続モデルである。連続モデルは強い非線的なシステムダイナミクスを捉えにくく、構成する要素間の相互作用も反映しないという欠点があり、複雑系のモデル化に適していないといえる。これに対して、我々はSCSのモデリングとして離散モデルを採用している。
離散モデル成立の前提
統計物理領域での1つの観測
システム全体のダイナミクスはシステムを構成する要素の振る舞いの細部に影響されない
例えば、水の分子世界と空気の分子世界は全く違うと言えるが、水の流れと空気の流れは似ていて、同じ形の方程式に支配されている。
離散モデルの構築
システムの構成要素における抽象化モデリング
例えば
- 流体分子や、コロイドや、界面活性剤分子などを粒子/セルとしてモデリング行う
- ヒューマンや、組織などをエージェント/ノードとしてモデリングを行う
システムの構成要素間の相互作用における抽象化モデリング
例えば
- 分子間力を粒子衝突としてモデリングを行う
- 人間の意思決定をエージェントのゲーム戦略として、人間の順応性をエージェントの帰納学習としてモデリングを行う
離散モデルを用いたシミュレーションによるシステムの全体挙動の再現
離散モデル成立の前提によれば、適切にシステム構成要素の抽象化モデリングが行われる場合、シミュレーションによるシステムの全体挙動を再現できる。それだけでなく、システムの全体挙動の背後に働いている機構や、システム内部に存在する構造などを解明することも可能である。
離散モデルの実例
複雑物理系を代表する複雑流体の離散粒子モデル、複雑適応系を代表する金融市場のGCMGモデルを紹介する。
離散粒子モデル
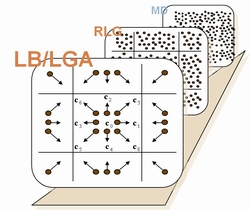
・格子ボルツマンモデル(Lattice Boltzmann Method, LBM)
・実数格子ガスモデル(Real-Coded Lattice Gas, RLG)
・モデルの特徴
- 流体分子運動の離散化
- マクロの保存則と等向性に対応するミクロの保存則と対称性
- 離散運動論による解析可能
GCMGモデル
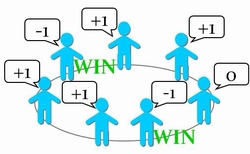
・Grand Canonical Minority Game (GCMG)モデル
・Minority Game (MG)からの拡張
・モデルの特徴
- 不完全情報ベースのエージェント意思決定
- エージェントのゲーム参加戦略の多様性
- 帰納学習によるエージェントの適応能力
- 市場参加の本質を反映する少数派有利な利得関数
- 市場参加の閾値
SCS laboratory
住所
〒277-8563 千葉県柏市柏の葉5-1-5 環境棟216号室
TEL/FAX/E-Mail
04-7136-4603 (東大内線64603)
chen@edu.k.u-tokyo.ac.jp
